Jittor Backend Example: Model Fusion by Graph Matching

This example shows how to fuse different models into a single model by pygmtools. Model fusion aims to fuse multiple models into one, such that the fused model could have higher performance. The neural networks can be regarded as graphs (channels - nodes, update functions between channels - edges; node feature - bias, edge feature - weights), and fusing the models is equivalent to solving a graph matching problem. In this example, the given models are trained on MNIST data from different distributions, and the fused model could combine the knowledge from two input models and can reach higher accuracy when testing.

# Author: Chang Liu <only-changer@sjtu.edu.cn>
#         Runzhong Wang <runzhong.wang@sjtu.edu.cn>
#         Wenzheng Pan <pwz1121@sjtu.edu.cn>
#
# License: Mulan PSL v2 License

Note

This is a simplified implementation of the ideas in Liu et al. Deep Neural Network Fusion via Graph Matching with Applications to Model Ensemble and Federated Learning. ICML 2022. For more details, please refer to the paper and the official code repository.

Note

The following solvers are included in this example:

• sm() (classic solver)

• hungarian() (linear solver)

import jittor as jt
import jittor.nn as nn
from jittor import Module, transform, dataset
import time
from PIL import Image
import matplotlib.pyplot as plt
import pygmtools as pygm

pygm.set_backend('jittor')

Define a simple CNN classifier network

class SimpleNet(Module):
    def __init__(self):
        super(SimpleNet, self).__init__()
        # self.pad = nn.ReplicationPad2d(1)
        self.conv1 = nn.Conv2d(1, 32, 5, bias=False)
        self.max_pool = nn.MaxPool2d(2, padding=1)
        self.conv2 = nn.Conv2d(32, 64, 5, bias=False)
        self.fc1 = nn.Linear(3136, 32, bias=False)
        self.fc2 = nn.Linear(32, 10, bias=False)

    def execute(self, x):
        output = nn.relu(self.conv1(nn.ReplicationPad2d(1)(x)))
        output = self.max_pool(output)
        output = nn.relu(self.conv2(nn.ReplicationPad2d(1)(output)))
        output = self.max_pool(output)
        output = output.view(output.shape[0], -1)
        output = self.fc1(output)
        output = self.fc2(output)
        return output

Load the trained models to be fused

model1 = SimpleNet()
model2 = SimpleNet()
model1.load_state_dict(jt.load('../data/example_model_fusion_1_jittor.dat'))
model2.load_state_dict(jt.load('../data/example_model_fusion_2_jittor.dat'))
test_transform = transform.Compose([
    transform.Gray(),
    transform.ToTensor()
])
test_dataset = dataset.MNIST(
    data_root='../data/mnist_data_jittor/',  # the directory to store the dataset
    train=False,  # the dataset is used to test
    transform=test_transform,  # the dataset is in the form of tensors
    download=True)
test_loader = test_dataset.set_attrs(batch_size=32, shuffle=False)

Print the layers of the simple CNN model:

print(model1)

SimpleNet(
    conv1: Conv(1, 32, (5, 5), (1, 1), (0, 0), (1, 1), 1, None, None, Kw=None, fan=None, i=None, bound=None)
    max_pool: MaxPool2d(
        _layer: Pool((2, 2), (2, 2), padding=(1, 1), dilation=None, return_indices=None, ceil_mode=False, count_include_pad=True, op=maximum)
    )
    conv2: Conv(32, 64, (5, 5), (1, 1), (0, 0), (1, 1), 1, None, None, Kw=None, fan=None, i=None, bound=None)
    fc1: Linear(3136, 32, None, None)
    fc2: Linear(32, 10, None, None)
)

Test the input models

with jt.no_grad():
    n_correct1 = 0
    n_correct2 = 0
    n_samples = 0
    for images, labels in test_loader:
        outputs1 = model1(images)
        outputs2 = model2(images)
        predictions1, _ = jt.argmax(outputs1, 1)
        predictions2, _ = jt.argmax(outputs2, 1)
        n_samples += labels.shape[0]
        n_correct1 += (predictions1 == labels).sum().item()
        n_correct2 += (predictions2 == labels).sum().item()
    acc1 = 100 * n_correct1 / n_samples
    acc2 = 100 * n_correct2 / n_samples

Testing results (two separate models):

print(f'model1 accuracy = {acc1}%, model2 accuracy = {acc2}%')

model1 accuracy = 84.18%, model2 accuracy = 83.81%

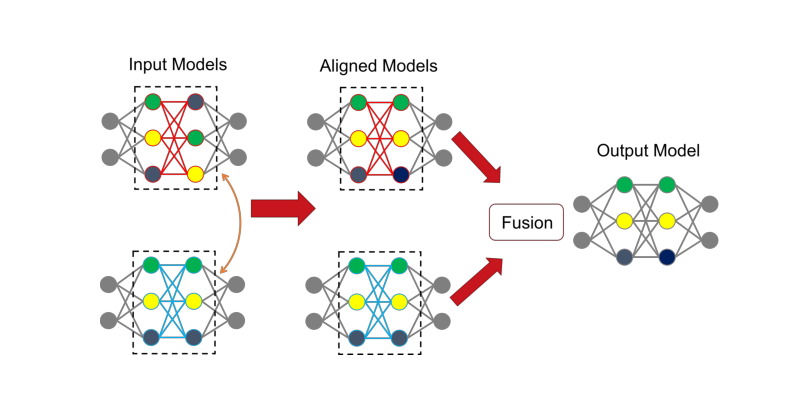
Build the affinity matrix for graph matching

As shown in the following plot, the neural networks can be regarded as graphs. The weights correspond to the edge features, and the bias corresponds to the node features. In this example, the neural network does not have bias so that there are only edge features.

plt.figure(figsize=(8, 4))
img = Image.open('../data/model_fusion.png')
plt.imshow(img)
plt.axis('off')
st_time = time.perf_counter()

Define the graph matching affinity metric function

class Ground_Metric_GM:
    def __init__(self,
                 model_1_param: jt.Var = None,
                 model_2_param: jt.Var = None,
                 conv_param: bool = False,
                 bias_param: bool = False,
                 pre_conv_param: bool = False,
                 pre_conv_image_size_squared: int = None):
        self.model_1_param = model_1_param
        self.model_2_param = model_2_param
        self.conv_param = conv_param
        self.bias_param = bias_param
        # bias, or fully-connected from linear
        if bias_param is True or (conv_param is False and pre_conv_param is False):
            self.model_1_param = self.model_1_param.reshape(1, -1, 1)
            self.model_2_param = self.model_2_param.reshape(1, -1, 1)
        # fully-connected from conv
        elif conv_param is False and pre_conv_param is True:
            self.model_1_param = self.model_1_param.reshape(1, -1, pre_conv_image_size_squared)
            self.model_2_param = self.model_2_param.reshape(1, -1, pre_conv_image_size_squared)
        # conv
        else:
            self.model_1_param = self.model_1_param.reshape(1, -1, model_1_param.shape[-1])
            self.model_2_param = self.model_2_param.reshape(1, -1, model_2_param.shape[-1])

    def _cdist(self, x1, x2, p = 2):
        assert len(x1.shape) == len(x2.shape) == 3 and x1.shape[-1] == x2.shape[-1]  # actual shape here: [1, 32, 25]
        dist = jt.zeros((x1.shape[0], x1.shape[1], x2.shape[1]))
        assert p == 2
        for i in range(x1.shape[0]):
            for j in range(x1.shape[1]):
                for k in range(x2.shape[1]):
                    dist[i, j, k] = (x1[i][j] - x2[i][k]).pow(2).sum().sqrt().item()
        return dist

    def process_distance(self, p: int = 2):
        return self._cdist(
            self.model_1_param.float(),
            self.model_2_param.float(),
            p=p)[0]

    def process_soft_affinity(self, p: int = 2):
        return jt.exp(0 - self.process_distance(p=p))

Define the affinity function between two neural networks. This function takes multiple neural network modules, and construct the corresponding affinity matrix which is further processed by the graph matching solver.

def graph_matching_fusion(networks: list):
    def total_node_num(network: jt.nn.Module):
        # count the total number of nodes in the network [network]
        num_nodes = 0
        for idx, (name, parameters) in enumerate(network.named_parameters()):
            if 'bias' in name:
                continue
            if idx == 0:
                num_nodes += parameters.shape[1]
            num_nodes += parameters.shape[0]
        return num_nodes

    n1 = total_node_num(network=networks[0])
    n2 = total_node_num(network=networks[1])
    assert (n1 == n2)
    affinity = jt.zeros([n1 * n2, n1 * n2])
    num_layers = len(list(zip(networks[0].parameters(), networks[1].parameters())))
    num_nodes_before = 0
    num_nodes_incremental = []
    num_nodes_layers = []
    pre_conv_list = []
    cur_conv_list = []
    conv_kernel_size_list = []
    num_nodes_pre = 0
    is_conv = False
    pre_conv = False
    pre_conv_out_channel = 1
    is_final_bias = False
    perm_is_complete = True
    named_weight_list_0 = [named_parameter for named_parameter in networks[0].named_parameters()]
    for idx, ((_, fc_layer0_weight), (_, fc_layer1_weight)) in \
            enumerate(zip(networks[0].named_parameters(), networks[1].named_parameters())):
        assert fc_layer0_weight.shape == fc_layer1_weight.shape
        layer_shape = fc_layer0_weight.shape
        num_nodes_cur = fc_layer0_weight.shape[0]
        if len(layer_shape) > 1:
            if is_conv is True and len(layer_shape) == 2:
                num_nodes_pre = pre_conv_out_channel
            else:
                num_nodes_pre = fc_layer0_weight.shape[1]
        if idx >= 1 and len(named_weight_list_0[idx - 1][1].shape) == 1:
            pre_bias = True
        else:
            pre_bias = False
        if len(layer_shape) > 2:
            is_bias = False
            if not pre_bias:
                pre_conv = is_conv
                pre_conv_list.append(pre_conv)
            is_conv = True
            cur_conv_list.append(is_conv)
            fc_layer0_weight_data = fc_layer0_weight.data.reshape(fc_layer0_weight.shape[0], fc_layer0_weight.shape[1], -1)
            fc_layer1_weight_data = fc_layer1_weight.data.reshape(fc_layer1_weight.shape[0], fc_layer1_weight.shape[1], -1)
        elif len(layer_shape) == 2:
            is_bias = False
            if not pre_bias:
                pre_conv = is_conv
                pre_conv_list.append(pre_conv)
            is_conv = False
            cur_conv_list.append(is_conv)
            fc_layer0_weight_data = fc_layer0_weight.data
            fc_layer1_weight_data = fc_layer1_weight.data
        else:
            is_bias = True
            if not pre_bias:
                pre_conv = is_conv
                pre_conv_list.append(pre_conv)
            is_conv = False
            cur_conv_list.append(is_conv)
            fc_layer0_weight_data = fc_layer0_weight.data
            fc_layer1_weight_data = fc_layer1_weight.data
        if is_conv:
            pre_conv_out_channel = num_nodes_cur
        if is_bias is True and idx == num_layers - 1:
            is_final_bias = True
        if idx == 0:
            for a in range(num_nodes_pre):
                affinity[(num_nodes_before + a) * n2 + num_nodes_before + a, \
                    (num_nodes_before + a) * n2 + num_nodes_before + a] \
                    = 1
        if idx == num_layers - 2 and 'bias' in named_weight_list_0[idx + 1][0] or \
                idx == num_layers - 1 and 'bias' not in named_weight_list_0[idx][0]:
            for a in range(num_nodes_cur):
                affinity[(num_nodes_before + num_nodes_pre + a) * n2 + num_nodes_before + num_nodes_pre + a, \
                    (num_nodes_before + num_nodes_pre + a) * n2 + num_nodes_before + num_nodes_pre + a] \
                    = 1
        if is_bias is False:
            ground_metric = Ground_Metric_GM(
                jt.Var(fc_layer0_weight_data), jt.Var(fc_layer1_weight_data), is_conv, is_bias,
                pre_conv, int(fc_layer0_weight_data.shape[1] / pre_conv_out_channel))
        else:
            ground_metric = Ground_Metric_GM(
                jt.Var(fc_layer0_weight_data), jt.Var(fc_layer1_weight_data), is_conv, is_bias,
                pre_conv, 1)

        layer_affinity = ground_metric.process_soft_affinity(p=2)

        if is_bias is False:
            pre_conv_kernel_size = fc_layer0_weight.shape[3] if is_conv else None
            conv_kernel_size_list.append(pre_conv_kernel_size)
        if is_bias is True and is_final_bias is False:
            for a in range(num_nodes_cur):
                for c in range(num_nodes_cur):
                    affinity[(num_nodes_before + a) * n2 + num_nodes_before + c, \
                        (num_nodes_before + a) * n2 + num_nodes_before + c] \
                        = layer_affinity[a][c]
        elif is_final_bias is False:
            for a in range(num_nodes_pre):
                for b in range(num_nodes_cur):
                    affinity[
                    (num_nodes_before + a) * n2 + num_nodes_before:
                    (num_nodes_before + a) * n2 + num_nodes_before + num_nodes_pre,
                    (num_nodes_before + num_nodes_pre + b) * n2 + num_nodes_before + num_nodes_pre:
                    (num_nodes_before + num_nodes_pre + b) * n2 + num_nodes_before + num_nodes_pre + num_nodes_cur] \
                        = layer_affinity[a + b * num_nodes_pre].view(num_nodes_cur, num_nodes_pre).transpose(0, 1)
        if is_bias is False:
            num_nodes_before += num_nodes_pre
            num_nodes_incremental.append(num_nodes_before)
            num_nodes_layers.append(num_nodes_cur)
    # affinity = (affinity + affinity.t()) / 2
    return affinity, [n1, n2, num_nodes_incremental, num_nodes_layers, cur_conv_list, conv_kernel_size_list]

Get the affinity (similarity) matrix between model1 and model2.

K, params = graph_matching_fusion([model1, model2])

Align the models by graph matching

Align the channels of model1 & model2 by maximize the affinity (similarity) via graph matching algorithms.

n1 = params[0]
n2 = params[1]
X = pygm.sm(K, n1, n2)

Project X to neural network matching result. The neural network matching matrix is built by applying Hungarian to small blocks of X, because only the channels from the same neural network layer can be matched.

Note

In this example, we assume the last FC layer is aligned and need not be matched.

new_X = jt.zeros_like(X)
new_X[:params[2][0], :params[2][0]] = jt.init.eye(params[2][0])
for start_idx, length in zip(params[2][:-1], params[3][:-1]):  # params[2] and params[3] are the indices of layers
    slicing = slice(start_idx, start_idx + length)
    new_X[slicing, slicing] = pygm.hungarian(X[slicing, slicing])
# assume the last FC layer is aligned
slicing = slice(params[2][-1], params[2][-1] + params[3][-1])
new_X[slicing, slicing] = jt.init.eye(params[3][-1])
X = new_X

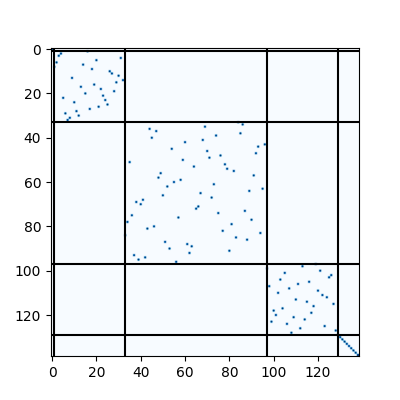
Visualization of the matching result. The black lines splits the channels of different layers.

plt.figure(figsize=(4, 4))
plt.imshow(X.numpy(), cmap='Blues')
for idx in params[2]:
    plt.axvline(x=idx, color='k')
    plt.axhline(y=idx, color='k')

Define the alignment function: fuse the models based on matching result

def align(solution, fusion_proportion, networks: list, params: list):
    [_, _, num_nodes_incremental, num_nodes_layers, cur_conv_list, conv_kernel_size_list] = params
    named_weight_list_0 = [named_parameter for named_parameter in networks[0].named_parameters()]
    aligned_wt_0 = [parameter.data for name, parameter in named_weight_list_0]
    idx = 0
    num_layers = len(aligned_wt_0)
    for num_before, num_cur, cur_conv, cur_kernel_size in \
            zip(num_nodes_incremental, num_nodes_layers, cur_conv_list, conv_kernel_size_list):
        perm = jt.Var(solution[num_before:num_before + num_cur, num_before:num_before + num_cur])
        assert 'bias' not in named_weight_list_0[idx][0]
        if len(named_weight_list_0[idx][1].shape) == 4:
            aligned_wt_0[idx] = (perm.transpose(0, 1).float32() @
                                 jt.Var(aligned_wt_0[idx]).float32().permute(2, 3, 0, 1)) \
                .permute(2, 3, 0, 1)
        else:
            aligned_wt_0[idx] = perm.transpose(0, 1).float32() @ jt.Var(aligned_wt_0[idx]).float32()
        idx += 1
        if idx >= num_layers:
            continue
        if 'bias' in named_weight_list_0[idx][0]:
            aligned_wt_0[idx] = jt.Var(aligned_wt_0[idx]).float32() @ perm.float32()
            idx += 1
        if idx >= num_layers:
            continue
        if cur_conv and len(named_weight_list_0[idx][1].shape) == 2:
            aligned_wt_0[idx] = (jt.Var(aligned_wt_0[idx]).float32()
                                 .reshape(aligned_wt_0[idx].shape[0], 64, -1)
                                 .permute(0, 2, 1)
                                 @ perm.float32()) \
                .permute(0, 2, 1) \
                .reshape(aligned_wt_0[idx].shape[0], -1)
        elif len(named_weight_list_0[idx][1].shape) == 4:
            aligned_wt_0[idx] = (jt.Var(aligned_wt_0[idx]).float32()
                                 .permute(2, 3, 0, 1)
                                 @ perm.float32()) \
                .permute(2, 3, 0, 1)
        else:
            aligned_wt_0[idx] = jt.Var(aligned_wt_0[idx]).float32() @ perm.float32()
    assert idx == num_layers

    averaged_weights = []
    for idx, parameter in enumerate(networks[1].parameters()):
        averaged_weights.append((1 - fusion_proportion) * aligned_wt_0[idx] + fusion_proportion * parameter)
    return averaged_weights

Test the fused model

The fusion_proportion variable denotes the contribution to the new model. For example, if fusion_proportion=0.2, the fused model = 80% model1 + 20% model2.

def align_model_and_test(X):
    acc_list = []
    for fusion_proportion in jt.arange(0, 1.1, 0.1):
        fused_weights = align(X, fusion_proportion, [model1, model2], params)
        fused_model = SimpleNet()
        state_dict = fused_model.state_dict()
        for idx, (key, _) in enumerate(state_dict.items()):
            state_dict[key] = fused_weights[idx]
        fused_model.load_state_dict(state_dict)
        test_loss = 0
        correct = 0
        for data, target in test_loader:
            output = fused_model(data)
            test_loss += nn.nll_loss(output, target, reduction='sum').item()
            pred = output.argmax(1, keepdims=True)[0]
            correct += pred.equal(target.view_as(pred)).sum()
        test_loss /= test_dataset.total_len
        acc = (100. * correct / test_dataset.total_len).item()
        print(
            f"{1 - fusion_proportion:.2f} model1 + {fusion_proportion:.2f} model2 -> fused model accuracy: {acc:.2f}%")
        acc_list.append(acc)
    return jt.Var(acc_list)


print('Graph Matching Fusion')
gm_acc_list = align_model_and_test(X)

Graph Matching Fusion
1.00 model1 + 0.00 model2 -> fused model accuracy: 84.18%
0.90 model1 + 0.10 model2 -> fused model accuracy: 85.12%
0.80 model1 + 0.20 model2 -> fused model accuracy: 85.21%
0.70 model1 + 0.30 model2 -> fused model accuracy: 82.52%
0.60 model1 + 0.40 model2 -> fused model accuracy: 71.11%
0.50 model1 + 0.50 model2 -> fused model accuracy: 53.74%
0.40 model1 + 0.60 model2 -> fused model accuracy: 63.26%
0.30 model1 + 0.70 model2 -> fused model accuracy: 78.51%
0.20 model1 + 0.80 model2 -> fused model accuracy: 82.81%
0.10 model1 + 0.90 model2 -> fused model accuracy: 83.97%
0.00 model1 + 1.00 model2 -> fused model accuracy: 83.81%

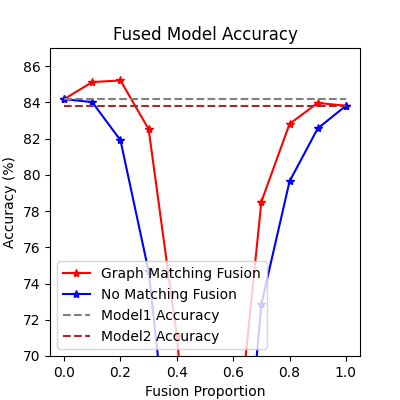
Compare with vanilla model fusion (no matching), graph matching method stabilizes the fusion step:

print('No Matching Fusion')
vanilla_acc_list = align_model_and_test(jt.init.eye(n1))

plt.figure(figsize=(4, 4))
plt.title('Fused Model Accuracy')
plt.plot(jt.arange(0, 1.1, 0.1).numpy(), gm_acc_list.numpy(), 'r*-', label='Graph Matching Fusion')
plt.plot(jt.arange(0, 1.1, 0.1).numpy(), vanilla_acc_list.numpy(), 'b*-', label='No Matching Fusion')
plt.plot(jt.arange(0, 1.1, 0.1).numpy(), [acc1] * 11, '--', color="gray", label='Model1 Accuracy')
plt.plot(jt.arange(0, 1.1, 0.1).numpy(), [acc2] * 11, '--', color="brown", label='Model2 Accuracy')
plt.gca().set_xlabel('Fusion Proportion')
plt.gca().set_ylabel('Accuracy (%)')
plt.ylim((70, 87))
plt.legend(loc=3)
plt.show()

No Matching Fusion
1.00 model1 + 0.00 model2 -> fused model accuracy: 84.18%
0.90 model1 + 0.10 model2 -> fused model accuracy: 84.01%
0.80 model1 + 0.20 model2 -> fused model accuracy: 81.91%
0.70 model1 + 0.30 model2 -> fused model accuracy: 74.67%
0.60 model1 + 0.40 model2 -> fused model accuracy: 60.39%
0.50 model1 + 0.50 model2 -> fused model accuracy: 47.16%
0.40 model1 + 0.60 model2 -> fused model accuracy: 55.34%
0.30 model1 + 0.70 model2 -> fused model accuracy: 72.86%
0.20 model1 + 0.80 model2 -> fused model accuracy: 79.64%
0.10 model1 + 0.90 model2 -> fused model accuracy: 82.56%
0.00 model1 + 1.00 model2 -> fused model accuracy: 83.81%

Print the result summary

end_time = time.perf_counter()
print(f'time consumed for model fusion: {end_time - st_time:.2f} seconds')
print(f'model1 accuracy = {acc1}%, model2 accuracy = {acc2}%')
print(f"best fused model accuracy: {jt.max(gm_acc_list):.2f}%")

time consumed for model fusion: 192.60 seconds
model1 accuracy = 84.18%, model2 accuracy = 83.81%
best fused model accuracy: 85.21%

Note

This example supports both GPU and CPU, and the online documentation is built by a CPU-only machine. The efficiency will be significantly improved if you run this code on GPU.