Note

Go to the end to download the full example code

PyTorch Backend Example: Matching Image Keypoints by Graph Matching Neural Networks

This example shows how to match image keypoints by neural network-based graph matching solvers. These graph matching solvers are designed to match two individual graphs. The matched images can be further passed to tackle downstream tasks.

# Author: Runzhong Wang <runzhong.wang@sjtu.edu.cn>
#
# License: Mulan PSL v2 License

Note

The following solvers are based on matching two individual graphs, and are included in this example:

pca_gm() (neural network solver)
ipca_gm() (neural network solver)
cie() (neural network solver)

import torch # pytorch backend
import torchvision # CV models
import pygmtools as pygm
import matplotlib.pyplot as plt # for plotting
from matplotlib.patches import ConnectionPatch # for plotting matching result
import scipy.io as sio # for loading .mat file
import scipy.spatial as spa # for Delaunay triangulation
from sklearn.decomposition import PCA as PCAdimReduc
import itertools
import numpy as np
from PIL import Image
pygm.set_backend('pytorch') # set default backend for pygmtools

Predicting Matching by Graph Matching Neural Networks

In this section we show how to do predictions (inference) by graph matching neural networks. Let’s take PCA-GM (pca_gm()) as an example.

Load the images

Images are from the Willow Object Class dataset (this dataset also available with the Benchmark of pygmtools, see WillowObject).

The images are resized to 256x256.

obj_resize = (256, 256)
img1 = Image.open('../data/willow_duck_0001.png')
img2 = Image.open('../data/willow_duck_0002.png')
kpts1 = torch.tensor(sio.loadmat('../data/willow_duck_0001.mat')['pts_coord'])
kpts2 = torch.tensor(sio.loadmat('../data/willow_duck_0002.mat')['pts_coord'])
kpts1[0] = kpts1[0] * obj_resize[0] / img1.size[0]
kpts1[1] = kpts1[1] * obj_resize[1] / img1.size[1]
kpts2[0] = kpts2[0] * obj_resize[0] / img2.size[0]
kpts2[1] = kpts2[1] * obj_resize[1] / img2.size[1]
img1 = img1.resize(obj_resize, resample=Image.BILINEAR)
img2 = img2.resize(obj_resize, resample=Image.BILINEAR)
torch_img1 = torch.from_numpy(np.array(img1, dtype=np.float32) / 256).permute(2, 0, 1).unsqueeze(0) # shape: BxCxHxW
torch_img2 = torch.from_numpy(np.array(img2, dtype=np.float32) / 256).permute(2, 0, 1).unsqueeze(0) # shape: BxCxHxW

Visualize the images and keypoints

def plot_image_with_graph(img, kpt, A=None):
    plt.imshow(img)
    plt.scatter(kpt[0], kpt[1], c='w', edgecolors='k')
    if A is not None:
        for idx in torch.nonzero(A, as_tuple=False):
            plt.plot((kpt[0, idx[0]], kpt[0, idx[1]]), (kpt[1, idx[0]], kpt[1, idx[1]]), 'k-')

plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
plt.title('Image 1')
plot_image_with_graph(img1, kpts1)
plt.subplot(1, 2, 2)
plt.title('Image 2')
plot_image_with_graph(img2, kpts2)

Build the graphs

Graph structures are built based on the geometric structure of the keypoint set. In this example, we refer to Delaunay triangulation.

def delaunay_triangulation(kpt):
    d = spa.Delaunay(kpt.numpy().transpose())
    A = torch.zeros(len(kpt[0]), len(kpt[0]))
    for simplex in d.simplices:
        for pair in itertools.permutations(simplex, 2):
            A[pair] = 1
    return A

A1 = delaunay_triangulation(kpts1)
A2 = delaunay_triangulation(kpts2)

Visualize the graphs

plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
plt.title('Image 1 with Graphs')
plot_image_with_graph(img1, kpts1, A1)
plt.subplot(1, 2, 2)
plt.title('Image 2 with Graphs')
plot_image_with_graph(img2, kpts2, A2)

Image 1 with Graphs, Image 2 with Graphs

Extract node features via CNN

Deep graph matching solvers can be fused with CNN feature extractors, to build an end-to-end learning pipeline.

In this example, let’s adopt the deep graph solvers based on matching two individual graphs. The image features are based on two intermediate layers from the VGG16 CNN model, following existing deep graph matching papers (such as pca_gm())

Let’s firstly fetch and download the VGG16 model:

vgg16_cnn = torchvision.models.vgg16_bn(True)

List of layers of VGG16:

print(vgg16_cnn.features)

Sequential(
  (0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (2): ReLU(inplace=True)
  (3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (5): ReLU(inplace=True)
  (6): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (7): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (8): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (9): ReLU(inplace=True)
  (10): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (11): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (12): ReLU(inplace=True)
  (13): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (14): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (15): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (16): ReLU(inplace=True)
  (17): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (18): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (19): ReLU(inplace=True)
  (20): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (21): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (22): ReLU(inplace=True)
  (23): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (24): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (25): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (26): ReLU(inplace=True)
  (27): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (28): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (29): ReLU(inplace=True)
  (30): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (31): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (32): ReLU(inplace=True)
  (33): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (34): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (35): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (36): ReLU(inplace=True)
  (37): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (38): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (39): ReLU(inplace=True)
  (40): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (41): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (42): ReLU(inplace=True)
  (43): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)

Let’s define the CNN feature extractor, which outputs the features of layer (30) and layer (37)

class CNNNet(torch.nn.Module):
    def __init__(self, vgg16_module):
        super(CNNNet, self).__init__()
        # The naming of the layers follow ThinkMatch convention to load pretrained models.
        self.node_layers = torch.nn.Sequential(*[_ for _ in vgg16_module.features[:31]])
        self.edge_layers = torch.nn.Sequential(*[_ for _ in vgg16_module.features[31:38]])

    def forward(self, inp_img):
        feat_local = self.node_layers(inp_img)
        feat_global = self.edge_layers(feat_local)
        return feat_local, feat_global

Download pretrained CNN weights (from ThinkMatch), load the weights and then extract the CNN features

cnn = CNNNet(vgg16_cnn)
path = pygm.utils.download('vgg16_pca_voc_pytorch.pt', 'https://drive.google.com/u/0/uc?export=download&confirm=Z-AR&id=1JnX3cSPvRYBSrDKVwByzp7CADgVCJCO_')
if torch.cuda.is_available():
    map_location = torch.device('cuda:0')
else:
    map_location = torch.device('cpu')
cnn.load_state_dict(torch.load(path, map_location=map_location), strict=False)
with torch.set_grad_enabled(False):
    feat1_local, feat1_global = cnn(torch_img1)
    feat2_local, feat2_global = cnn(torch_img2)

Normalize the features

def l2norm(node_feat):
    return torch.nn.functional.local_response_norm(
        node_feat, node_feat.shape[1] * 2, alpha=node_feat.shape[1] * 2, beta=0.5, k=0)

feat1_local = l2norm(feat1_local)
feat1_global = l2norm(feat1_global)
feat2_local = l2norm(feat2_local)
feat2_global = l2norm(feat2_global)

Up-sample the features to the original image size and concatenate

feat1_local_upsample = torch.nn.functional.interpolate(feat1_local, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat1_global_upsample = torch.nn.functional.interpolate(feat1_global, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat2_local_upsample = torch.nn.functional.interpolate(feat2_local, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat2_global_upsample = torch.nn.functional.interpolate(feat2_global, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat1_upsample = torch.cat((feat1_local_upsample, feat1_global_upsample), dim=1)
feat2_upsample = torch.cat((feat2_local_upsample, feat2_global_upsample), dim=1)
num_features = feat1_upsample.shape[1]

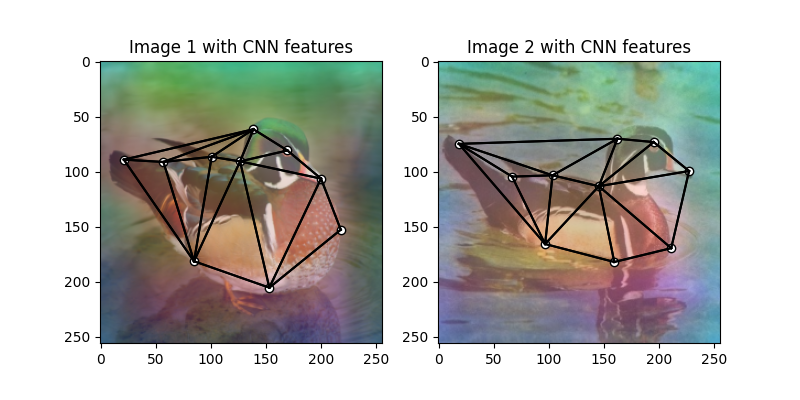
Visualize the extracted CNN feature (dimensionality reduction via principle component analysis)

pca_dim_reduc = PCAdimReduc(n_components=3, whiten=True)
feat_dim_reduc = pca_dim_reduc.fit_transform(
    np.concatenate((
        feat1_upsample.permute(0, 2, 3, 1).reshape(-1, num_features).numpy(),
        feat2_upsample.permute(0, 2, 3, 1).reshape(-1, num_features).numpy()
    ), axis=0)
)
feat_dim_reduc = feat_dim_reduc / np.max(np.abs(feat_dim_reduc), axis=0, keepdims=True) / 2 + 0.5
feat1_dim_reduc = feat_dim_reduc[:obj_resize[0] * obj_resize[1], :]
feat2_dim_reduc = feat_dim_reduc[obj_resize[0] * obj_resize[1]:, :]

plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
plt.title('Image 1 with CNN features')
plot_image_with_graph(img1, kpts1, A1)
plt.imshow(feat1_dim_reduc.reshape(obj_resize[1], obj_resize[0], 3), alpha=0.5)
plt.subplot(1, 2, 2)
plt.title('Image 2 with CNN features')
plot_image_with_graph(img2, kpts2, A2)
plt.imshow(feat2_dim_reduc.reshape(obj_resize[1], obj_resize[0], 3), alpha=0.5)

Image 1 with CNN features, Image 2 with CNN features

<matplotlib.image.AxesImage object at 0x7fe196ff8b50>

Extract node features by nearest interpolation

rounded_kpts1 = torch.round(kpts1).to(dtype=torch.long)
rounded_kpts2 = torch.round(kpts2).to(dtype=torch.long)
node1 = feat1_upsample[0, :, rounded_kpts1[1], rounded_kpts1[0]].t() # shape: NxC
node2 = feat2_upsample[0, :, rounded_kpts2[1], rounded_kpts2[0]].t() # shape: NxC

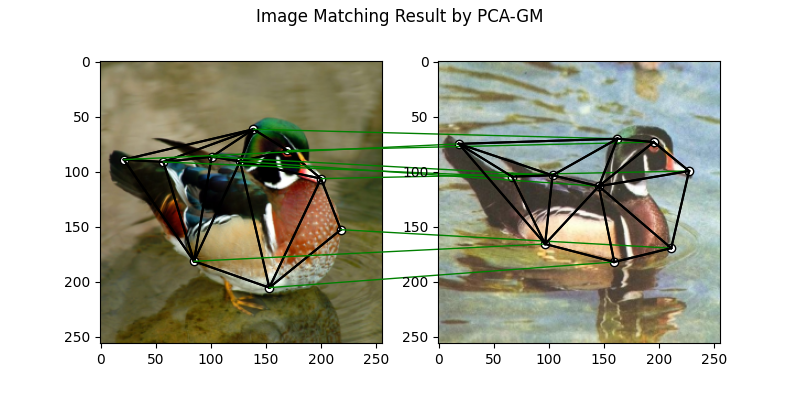
Call PCA-GM matching model

See pca_gm() for the API reference.

X = pygm.pca_gm(node1, node2, A1, A2, pretrain='voc')
X = pygm.hungarian(X)

plt.figure(figsize=(8, 4))
plt.suptitle('Image Matching Result by PCA-GM')
ax1 = plt.subplot(1, 2, 1)
plot_image_with_graph(img1, kpts1, A1)
ax2 = plt.subplot(1, 2, 2)
plot_image_with_graph(img2, kpts2, A2)
for i in range(X.shape[0]):
    j = torch.argmax(X[i]).item()
    con = ConnectionPatch(xyA=kpts1[:, i], xyB=kpts2[:, j], coordsA="data", coordsB="data",
                          axesA=ax1, axesB=ax2, color="red" if i != j else "green")
    plt.gca().add_artist(con)

Matching images with other neural networks

The above pipeline also works for other deep graph matching networks. Here we give examples of ipca_gm() and cie().

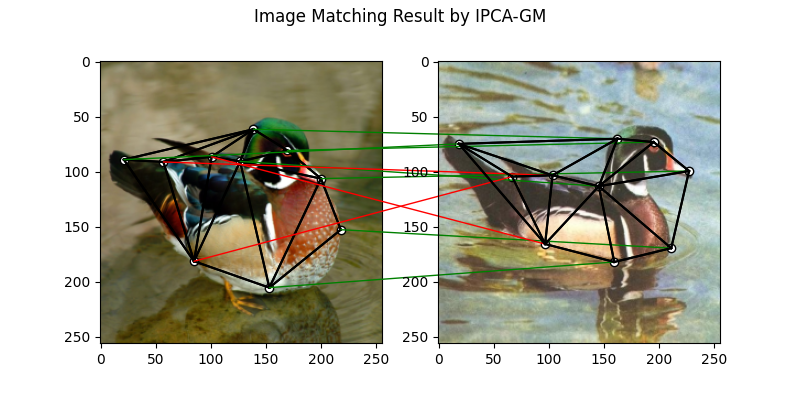
Matching by IPCA-GM model

See ipca_gm() for the API reference.

path = pygm.utils.download('vgg16_ipca_voc_pytorch.pt', 'https://drive.google.com/u/0/uc?export=download&confirm=Z-AR&id=1TGrbSQRmUkClH3Alz2OCwqjl8r8gf5yI')
cnn.load_state_dict(torch.load(path, map_location=map_location), strict=False)

with torch.set_grad_enabled(False):
    feat1_local, feat1_global = cnn(torch_img1)
    feat2_local, feat2_global = cnn(torch_img2)

Normalize the features

def l2norm(node_feat):
    return torch.nn.functional.local_response_norm(
        node_feat, node_feat.shape[1] * 2, alpha=node_feat.shape[1] * 2, beta=0.5, k=0)

feat1_local = l2norm(feat1_local)
feat1_global = l2norm(feat1_global)
feat2_local = l2norm(feat2_local)
feat2_global = l2norm(feat2_global)

Up-sample the features to the original image size and concatenate

feat1_local_upsample = torch.nn.functional.interpolate(feat1_local, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat1_global_upsample = torch.nn.functional.interpolate(feat1_global, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat2_local_upsample = torch.nn.functional.interpolate(feat2_local, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat2_global_upsample = torch.nn.functional.interpolate(feat2_global, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat1_upsample = torch.cat((feat1_local_upsample, feat1_global_upsample), dim=1)
feat2_upsample = torch.cat((feat2_local_upsample, feat2_global_upsample), dim=1)
num_features = feat1_upsample.shape[1]

Extract node features by nearest interpolation

rounded_kpts1 = torch.round(kpts1).to(dtype=torch.long)
rounded_kpts2 = torch.round(kpts2).to(dtype=torch.long)
node1 = feat1_upsample[0, :, rounded_kpts1[1], rounded_kpts1[0]].t() # shape: NxC
node2 = feat2_upsample[0, :, rounded_kpts2[1], rounded_kpts2[0]].t() # shape: NxC

Build edge features as edge lengths

kpts1_dis = (kpts1.unsqueeze(0) - kpts1.unsqueeze(1))
kpts1_dis = torch.norm(kpts1_dis, p=2, dim=2).detach()
kpts2_dis = (kpts2.unsqueeze(0) - kpts2.unsqueeze(1))
kpts2_dis = torch.norm(kpts2_dis, p=2, dim=2).detach()

Q1 = torch.exp(-kpts1_dis / obj_resize[0])
Q2 = torch.exp(-kpts2_dis / obj_resize[0])

Matching by IPCA-GM model

X = pygm.ipca_gm(node1, node2, A1, A2, pretrain='voc')
X = pygm.hungarian(X)

plt.figure(figsize=(8, 4))
plt.suptitle('Image Matching Result by IPCA-GM')
ax1 = plt.subplot(1, 2, 1)
plot_image_with_graph(img1, kpts1, A1)
ax2 = plt.subplot(1, 2, 2)
plot_image_with_graph(img2, kpts2, A2)
for i in range(X.shape[0]):
    j = torch.argmax(X[i]).item()
    con = ConnectionPatch(xyA=kpts1[:, i], xyB=kpts2[:, j], coordsA="data", coordsB="data",
                          axesA=ax1, axesB=ax2, color="red" if i != j else "green")
    plt.gca().add_artist(con)

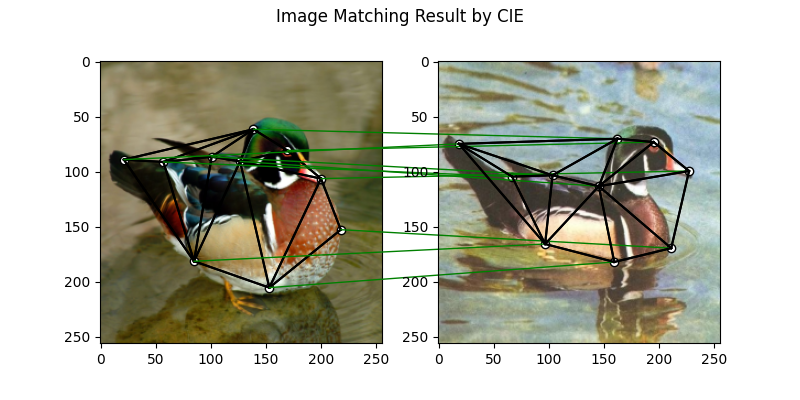
Matching by CIE model

See cie() for the API reference.

path = pygm.utils.download('vgg16_cie_voc_pytorch.pt', 'https://drive.google.com/u/0/uc?export=download&confirm=Z-AR&id=1oRwcnw06t1rCbrIN_7p8TJZY-XkBOFEp')
cnn.load_state_dict(torch.load(path, map_location=map_location), strict=False)

with torch.set_grad_enabled(False):
    feat1_local, feat1_global = cnn(torch_img1)
    feat2_local, feat2_global = cnn(torch_img2)

Normalize the features

def l2norm(node_feat):
    return torch.nn.functional.local_response_norm(
        node_feat, node_feat.shape[1] * 2, alpha=node_feat.shape[1] * 2, beta=0.5, k=0)

feat1_local = l2norm(feat1_local)
feat1_global = l2norm(feat1_global)
feat2_local = l2norm(feat2_local)
feat2_global = l2norm(feat2_global)

Up-sample the features to the original image size and concatenate

feat1_local_upsample = torch.nn.functional.interpolate(feat1_local, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat1_global_upsample = torch.nn.functional.interpolate(feat1_global, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat2_local_upsample = torch.nn.functional.interpolate(feat2_local, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat2_global_upsample = torch.nn.functional.interpolate(feat2_global, (obj_resize[1], obj_resize[0]), mode='bilinear')
feat1_upsample = torch.cat((feat1_local_upsample, feat1_global_upsample), dim=1)
feat2_upsample = torch.cat((feat2_local_upsample, feat2_global_upsample), dim=1)
num_features = feat1_upsample.shape[1]

Extract node features by nearest interpolation

rounded_kpts1 = torch.round(kpts1).to(dtype=torch.long)
rounded_kpts2 = torch.round(kpts2).to(dtype=torch.long)
node1 = feat1_upsample[0, :, rounded_kpts1[1], rounded_kpts1[0]].t() # shape: NxC
node2 = feat2_upsample[0, :, rounded_kpts2[1], rounded_kpts2[0]].t() # shape: NxC

Build edge features as edge lengths

kpts1_dis = (kpts1.unsqueeze(1) - kpts1.unsqueeze(2))
kpts1_dis = torch.norm(kpts1_dis, p=2, dim=0).detach()
kpts2_dis = (kpts2.unsqueeze(1) - kpts2.unsqueeze(2))
kpts2_dis = torch.norm(kpts2_dis, p=2, dim=0).detach()

Q1 = torch.exp(-kpts1_dis / obj_resize[0]).unsqueeze(-1).to(dtype=torch.float32)
Q2 = torch.exp(-kpts2_dis / obj_resize[0]).unsqueeze(-1).to(dtype=torch.float32)

Call CIE matching model

X = pygm.cie(node1, node2, A1, A2, Q1, Q2, pretrain='voc')
X = pygm.hungarian(X)

plt.figure(figsize=(8, 4))
plt.suptitle('Image Matching Result by CIE')
ax1 = plt.subplot(1, 2, 1)
plot_image_with_graph(img1, kpts1, A1)
ax2 = plt.subplot(1, 2, 2)
plot_image_with_graph(img2, kpts2, A2)
for i in range(X.shape[0]):
    j = torch.argmax(X[i]).item()
    con = ConnectionPatch(xyA=kpts1[:, i], xyB=kpts2[:, j], coordsA="data", coordsB="data",
                          axesA=ax1, axesB=ax2, color="red" if i != j else "green")
    plt.gca().add_artist(con)

Training a deep graph matching model

In this section, we show how to build a deep graph matching model which supports end-to-end training. For the image matching problem considered here, the model is composed of a CNN feature extractor and a learnable matching module. Take the PCA-GM model as an example.

Note

This simple example is intended to show you how to do the basic forward and backward pass when training an end-to-end deep graph matching neural network. A ‘more formal’ deep learning pipeline should involve asynchronized data loader, batched operations, CUDA support and so on, which are all omitted in consideration of simplicity. You may refer to ThinkMatch which is a research protocol with all these advanced features.

Let’s firstly define the neural network model. By calling get_network(), it will simply return the network object.

class GMNet(torch.nn.Module):
    def __init__(self):
        super(GMNet, self).__init__()
        self.gm_net = pygm.utils.get_network(pygm.pca_gm, pretrain=False) # fetch the network object
        self.cnn = CNNNet(vgg16_cnn)

    def forward(self, img1, img2, kpts1, kpts2, A1, A2):
        # CNN feature extractor layers
        feat1_local, feat1_global = self.cnn(img1)
        feat2_local, feat2_global = self.cnn(img2)
        feat1_local = l2norm(feat1_local)
        feat1_global = l2norm(feat1_global)
        feat2_local = l2norm(feat2_local)
        feat2_global = l2norm(feat2_global)

        # upsample feature map
        feat1_local_upsample = torch.nn.functional.interpolate(feat1_local, (obj_resize[1], obj_resize[0]), mode='bilinear')
        feat1_global_upsample = torch.nn.functional.interpolate(feat1_global, (obj_resize[1], obj_resize[0]), mode='bilinear')
        feat2_local_upsample = torch.nn.functional.interpolate(feat2_local, (obj_resize[1], obj_resize[0]), mode='bilinear')
        feat2_global_upsample = torch.nn.functional.interpolate(feat2_global, (obj_resize[1], obj_resize[0]), mode='bilinear')
        feat1_upsample = torch.cat((feat1_local_upsample, feat1_global_upsample), dim=1)
        feat2_upsample = torch.cat((feat2_local_upsample, feat2_global_upsample), dim=1)

        # assign node features
        rounded_kpts1 = torch.round(kpts1).to(dtype=torch.long)
        rounded_kpts2 = torch.round(kpts2).to(dtype=torch.long)
        node1 = feat1_upsample[0, :, rounded_kpts1[1], rounded_kpts1[0]].t()  # shape: NxC
        node2 = feat2_upsample[0, :, rounded_kpts2[1], rounded_kpts2[0]].t()  # shape: NxC

        # PCA-GM matching layers
        X = pygm.pca_gm(node1, node2, A1, A2, network=self.gm_net) # the network object is reused
        return X

model = GMNet()

Define optimizer

optim = torch.optim.Adam(model.parameters(), lr=1e-3)

Forward pass

X = model(torch_img1, torch_img2, kpts1, kpts2, A1, A2)

Compute loss

In this example, the ground truth matching matrix is a diagonal matrix. We calculate the loss function via permutation_loss()

X_gt = torch.eye(X.shape[0])
loss = pygm.utils.permutation_loss(X, X_gt)
print(f'loss={loss:.4f}')

loss=2.9619

Backward Pass

loss.backward()

Visualize the gradients

plt.figure(figsize=(4, 4))
plt.title('Gradient Sizes of PCA-GM and VGG16 layers')
plt.gca().set_xlabel('Layer Index')
plt.gca().set_ylabel('Average Gradient Size')
grad_size = []
for param in model.parameters():
    grad_size.append(torch.abs(param.grad).mean().item())
print(grad_size)
plt.stem(grad_size)

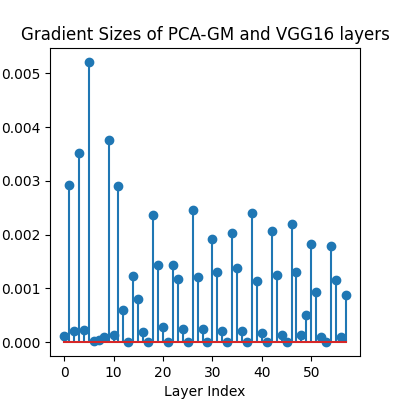
Gradient Sizes of PCA-GM and VGG16 layers

[0.00012030009384034202, 0.0029222508892416954, 0.00019840802997350693, 0.0035125715658068657, 0.00021948321955278516, 0.005211487412452698, 1.2157242963439785e-05, 4.538887151284143e-05, 9.093379776459187e-05, 0.003763300133869052, 0.00013752389349974692, 0.0029113302007317543, 0.0005891890614293516, 1.4391055458418123e-08, 0.00123009888920933, 0.0007960228249430656, 0.00019226272706873715, 7.602498186543016e-09, 0.0023636282421648502, 0.00142657570540905, 0.00027515203692018986, 2.3430166695703747e-09, 0.0014325324445962906, 0.001168975606560707, 0.000243743575992994, 3.208436183399499e-09, 0.002457045018672943, 0.0012053920654579997, 0.00024106756609398872, 9.623200014630129e-10, 0.0019094400340691209, 0.0013064424274489284, 0.00019915227312594652, 1.351938450078194e-09, 0.0020241807214915752, 0.0013774647377431393, 0.00020345798111520708, 1.4647631996211885e-09, 0.0024065959732979536, 0.0011330752167850733, 0.00017511722398921847, 4.4791811926181424e-10, 0.002062384970486164, 0.00124924979172647, 0.00013374598347581923, 5.668324698504534e-10, 0.002199235139414668, 0.0013085041427984834, 0.00012718267680611461, 0.0005019083619117737, 0.0018184399232268333, 0.0009283717372454703, 9.876605327008292e-05, 2.2953100531353243e-10, 0.0017888628644868731, 0.0011573054362088442, 8.91995950951241e-05, 0.0008793459855951369]

<StemContainer object of 3 artists>

Update the model parameters. A deep learning pipeline should iterate the forward pass and backward pass steps until convergence.

optim.step()
optim.zero_grad()

Note

This example supports both GPU and CPU, and the online documentation is built by a CPU-only machine. The efficiency will be significantly improved if you run this code on GPU.

Total running time of the script: (0 minutes 29.845 seconds)

Gallery generated by Sphinx-Gallery